Spatial regression models
Introduction
This chapter deals with the problem of inference in regression models with spatial data. Such inference can be suspect because, in essence, nearby things tend to be similar, and it may therefore not be fair to assume that nearby cases as independent of each other (they may be pseudo-replicates). Therefore, these models need to be diagnosed before reporting them. Specifically, it is important to evaluate the for spatial autocorrelation in the residuals (as these are supposed to be independent, not correlated).
If the residuals are spatially autocorrelated, this indicates that the model is misspecified. In that case you should try to improve the model by adding (and perhaps removing) important variables. If that is not possible (either because there is no data available, or because you have no clue as to what variable to look for), you can try formulating a regression model that controls for spatial autocorrelation. We show some examples of that approach here.
Reading & aggregating data
We use California house price data from the 2000 Census.
Get the data
if (!require("rspat")) remotes::install_github("rspatial/rspat")
## Loading required package: rspat
## Loading required package: terra
## terra 1.8.97
library(rspat)
h <- spat_data('houses2000')
I have selected some variables on on housing and population. You can get more data from the American Fact Finder http://factfinder2.census.gov (among other web sites).
dim(h)
## [1] 7049 29
names(h)
## [1] "TRACT" "GEOID" "label" "houseValue" "nhousingUn"
## [6] "recHouses" "nMobileHom" "yearBuilt" "nBadPlumbi" "nBadKitche"
## [11] "nRooms" "nBedrooms" "medHHinc" "Population" "Males"
## [16] "Females" "Under5" "MedianAge" "White" "Black"
## [21] "AmericanIn" "Asian" "Hispanic" "PopInHouse" "nHousehold"
## [26] "Families" "householdS" "familySize" "County"
These are the variables we have:
v ariable |
description |
|---|---|
nho usingUn |
number of housing units |
re cHouses |
number of houses for recreational use |
nMo bileHom |
number of mobile homes |
nBa dPlumbi |
number of houses with incomplete plumbing |
nBa dKitche |
number of houses with incomplete kitchens |
Pop ulation |
total population |
Males |
number of males |
Females |
number of females |
Under5 |
number of persons under five |
White |
number of persons identifying themselves as white (only) |
Black |
number of persons identifying themselves African-american (only) |
Ame ricanIn |
number of persons identifying themselves American Indian (only) |
Asian |
number of persons identifying themselves as American Indian (only) |
H ispanic |
number of persons identifying themselves as hispanic (only) |
Pop InHouse |
number of persons living in households |
nHo usehold |
number of households |
F amilies |
number of families |
hou seValue |
value of the house |
ye arBuilt |
year house was built |
nRooms |
median number of rooms per house |
nB edrooms |
median number of bedrooms per house |
m edHHinc |
median household income |
Me dianAge |
median age of population |
hou seholdS |
median household size |
fam ilySize |
median family size |
First some data massaging. These are values for Census tracts. I want to analyze these data at the county level. So we need to aggregate the values.
# using a tiny buffer to get a cleaner aggregation
hb <- buffer(h, 1)
values(hb) <- values(h)
hha <- aggregate(hb, "County")
Now we have the county outlines, but we also need to get the values of interest at the county level. Although it is possible to do everything in one step in the aggregate function, I prefer to do this step by step. The simplest case is where we can sum the numbers. For example for the number of houses.
d1 <- as.data.frame(h)[, c("nhousingUn", "recHouses", "nMobileHom", "nBadPlumbi",
"nBadKitche", "Population", "Males", "Females", "Under5", "White",
"Black", "AmericanIn", "Asian", "Hispanic", "PopInHouse", "nHousehold", "Families")]
d1a <- aggregate(d1, list(County=h$County), sum, na.rm=TRUE)
In other cases we need to use a weighted mean. For example for houseValue. We should weight it by the number of houses (households) in each tract.
d2 <- as.data.frame(h)[, c("houseValue", "yearBuilt", "nRooms", "nBedrooms",
"medHHinc", "MedianAge", "householdS", "familySize")]
d2 <- cbind(d2 * h$nHousehold, hh=h$nHousehold)
d2a <- aggregate(d2, list(County=h$County), sum, na.rm=TRUE)
d2a[, 2:ncol(d2a)] <- d2a[, 2:ncol(d2a)] / d2a$hh
Combine these two groups:
d12 <- merge(d1a, d2a, by='County')
And merge the aggregated (from census tract to county level) attribute data with the aggregated polygons
hh <- merge(hha[, "County"], d12, by='County')
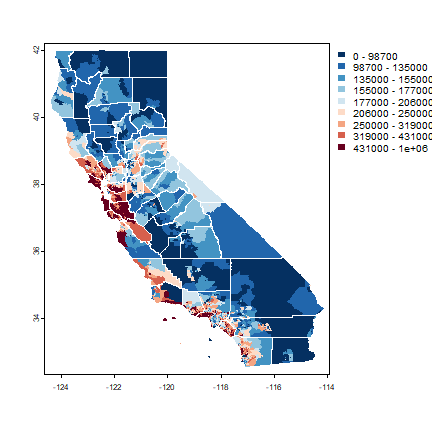
Let’s make some maps, at the orignal Census tract level. First the house value, using a legend with 10 intervals.
library(RColorBrewer)
grps <- 10
brks <- quantile(h$houseValue, 0:(grps-1)/(grps-1), na.rm=TRUE)
plot(h, "houseValue", breaks=brks, col=rev(brewer.pal(grps, "RdBu")), border=NA)
lines(hh, col="white")
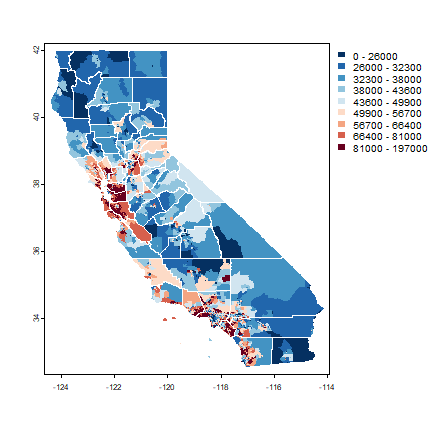
A map of the median household income.
brks <- quantile(h$medHHinc, 0:(grps-1)/(grps-1), na.rm=TRUE)
plot(h, "medHHinc", breaks=brks, col=rev(brewer.pal(grps, "RdBu")), border=NA)
lines(hh, col="white")
Basic OLS model
I now make some models with the county-level data. I first compute some new variables (that I might not all use).
hh$fBadP <- pmax(hh$nBadPlumbi, hh$nBadKitche) / hh$nhousingUn
hh$fWhite <- hh$White / hh$Population
hh$age <- 2000 - hh$yearBuilt
f1 <- houseValue ~ age + nBedrooms
m1 <- lm(f1, data=as.data.frame(hh))
summary(m1)
##
## Call:
## lm(formula = f1, data = as.data.frame(hh))
##
## Residuals:
## Min 1Q Median 3Q Max
## -222541 -67489 -6128 60509 217655
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -628578 233217 -2.695 0.00931 **
## age 12695 2480 5.119 4.05e-06 ***
## nBedrooms 191889 76756 2.500 0.01543 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 94740 on 55 degrees of freedom
## Multiple R-squared: 0.3235, Adjusted R-squared: 0.2989
## F-statistic: 13.15 on 2 and 55 DF, p-value: 2.147e-05
Just for illustration, here is how you can do OLS with matrix algebra. First set up the data. I add a constant variable ‘1’ to X, to get an intercept.
y <- matrix(hh$houseValue)
X <- cbind(1, hh$age, hh$nBedrooms)
Then use matrix algebra
ols <- solve(t(X) %*% X) %*% t(X) %*% y
rownames(ols) <- c('intercept', 'age', 'nBedroom')
ols
## [,1]
## intercept -628577.95
## age 12694.75
## nBedroom 191888.89
So, according to this simple model, “age” is highly significant. The older a house, the more expensive. You pay 1,269,475 dollars more for a house that is 100 years old than a for new house! While the p-value for the number of bedrooms is not impressive, but every bedroom adds about 200,000 dollars to the value of a house.
Question 1: What would be the price be of a house built in 1999 with three bedrooms?
(the answer may surprise you),
Let’s see if the errors (model residuals) appear to be randomly distributed in space.
hh$residuals <- residuals(m1)
brks <- quantile(hh$residuals, 0:(grps-1)/(grps-1), na.rm=TRUE)
plot(hh, "residuals", breaks=brks, col=rev(brewer.pal(grps, "RdBu")))
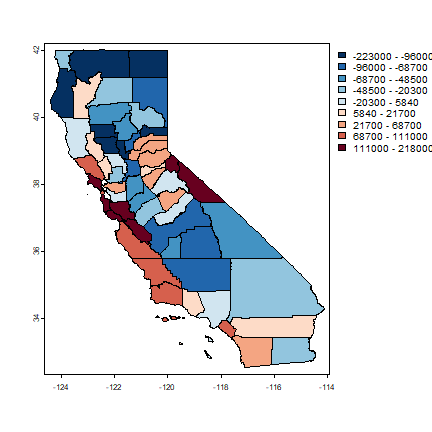
What do think? Is this a random pattern? Let’s see what Mr. Moran would say. First make a neighborhoods list. I add two links: between San Francisco and Marin County and vice versa (to consider the Golden Gate bridge).
library(spdep)
sfhh <- sf::st_as_sf(hh)
nb <- poly2nb(sfhh, snap=1/120)
## Error in wk_handle.wk_wkb(wkb, s2_geography_writer(oriented = oriented, : Loop 0 is not valid: Edge 198 is degenerate (duplicate vertex)
nb[[21]] <- sort(as.integer(c(nb[[21]], 38)))
## Error in h(simpleError(msg, call)): error in evaluating the argument 'x' in selecting a method for function 'sort': object 'nb' not found
nb[[38]] <- sort(as.integer(c(21, nb[[38]])))
## Error in h(simpleError(msg, call)): error in evaluating the argument 'x' in selecting a method for function 'sort': object 'nb' not found
nb
## Error: object 'nb' not found
par(mai=c(0,0,0,0))
plot(hh)
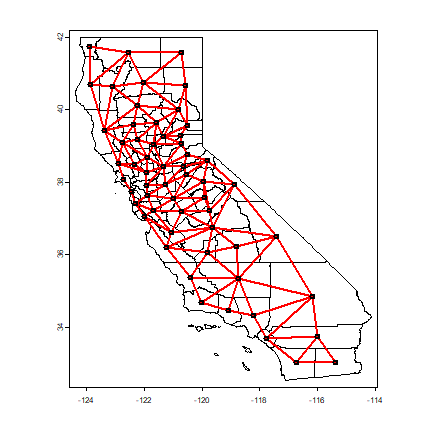
plot(nb, crds(centroids(hh)), col='red', lwd=2, add=TRUE)
## Error in h(simpleError(msg, call)): error in evaluating the argument 'x' in selecting a method for function 'plot': object 'nb' not found
We can use the neighbour list object to get the average value for the neighbors of each polygon.
resnb <- sapply(nb, function(x) mean(hh$residuals[x]))
## Error: object 'nb' not found
cor(hh$residuals, resnb)
## Error: object 'resnb' not found
plot(hh$residuals, resnb, xlab="Residuals", ylab="Mean adjacent residuals", pch=20)
## Error in h(simpleError(msg, call)): error in evaluating the argument 'y' in selecting a method for function 'plot': object 'resnb' not found
abline(lm(resnb ~ hh$residuals), lwd=2, lty=2)
## Error in eval(predvars, data, env): object 'resnb' not found
The residualso appear to be autocorrelated. A formal test:
lw <- nb2listw(nb)
## Error: object 'nb' not found
moran.mc(hh$residuals, lw, 999)
## Error: object 'lw' not found
Clearly, there is spatial autocorrelation. Our model cannot be trusted. so let’s try SAR models.
Spatial lag model
Here I show a how to do spatial regression with a spatial lag model
(lagsarlm), using the spatialreg package.
library(spatialreg )
m1s <- lagsarlm(f1, data=as.data.frame(hh), lw, tol.solve=1.0e-30)
## Error: object 'lw' not found
summary(m1s)
## Error in h(simpleError(msg, call)): error in evaluating the argument 'object' in selecting a method for function 'summary': object 'm1s' not found
hh$residuals <- residuals(m1s)
## Error: object 'm1s' not found
moran.mc(hh$residuals, lw, 999)
## Error: object 'lw' not found
brks <- quantile(hh$residuals, 0:(grps-1)/(grps-1), na.rm=TRUE)
plot(hh, "residuals", breaks=brks, col=rev(brewer.pal(grps, "RdBu")))
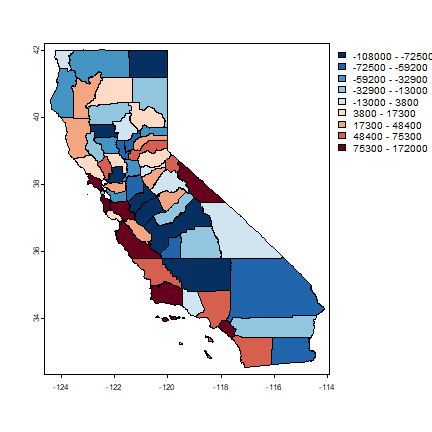
Spatial error model
And now with a “Spatial error” (or spatial moving average) models
(errorsarlm). Note the use of the lw argument.
m1e <- errorsarlm(f1, data=as.data.frame(hh), lw, tol.solve=1.0e-30)
## Error: object 'lw' not found
summary(m1e)
## Error in h(simpleError(msg, call)): error in evaluating the argument 'object' in selecting a method for function 'summary': object 'm1e' not found
hh$residuals <- residuals(m1e)
## Error: object 'm1e' not found
moran.mc(hh$residuals, lw, 999)
## Error: object 'lw' not found
brks <- quantile(hh$residuals, 0:(grps-1)/(grps-1), na.rm=TRUE)
plot(hh, "residuals", breaks=brks, col=rev(brewer.pal(grps, "RdBu")))
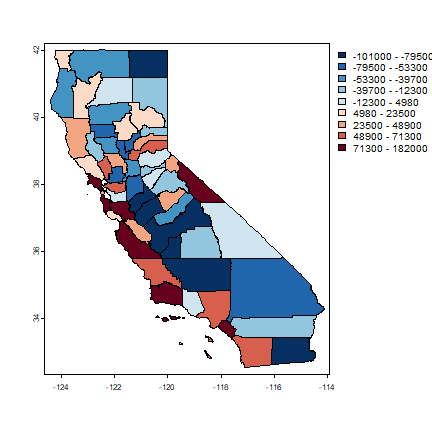
Are the residuals spatially auto-correlated for either of these models? Let’s plot them for the spatial error model.
brks <- quantile(hh$residuals, 0:(grps-1)/(grps-1), na.rm=TRUE)
plot(hh, "residuals", breaks=brks, col=rev(brewer.pal(grps, "RdBu")))
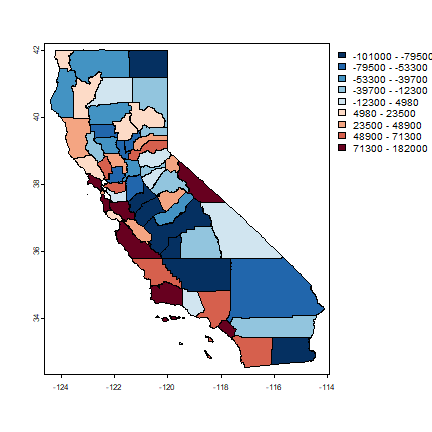
Questions
Question 2: The last two maps still seem to show a lot of spatial autocorrelation. But according to the tests there is none. Now why might that be?
Question 3: One of the most important, or perhaps THE most important aspect of modeling is variable selection. A misspecified model is never going to be any good, no matter how much you do to, e.g., correct for spatial autocorrelation.
Which variables would you choose from the list?
Which new variables could you propose to create from the variables in the list.
Which other variables could you add, created from the geometries/location (perhaps other geographic data).
add a lot of variables and use stepAIC to select an ‘optimal’ OLS model
check for spatial autocorrelation in the residuals of that model