Local regression
Regression models are typically “global”. That is, all date are used simultaneously to fit a single model. In some cases it can make sense to fit more flexible “local” models. Such models exist in a general regression framework (e.g. generalized additive models), where “local” refers to the values of the predictor values. In a spatial context local refers to location. Rather than fitting a single regression model, it is possible to fit several models, one for each location (out of possibly very many) locations. This technique is sometimes called “geographically weighted regression” (GWR). GWR is a data exploration technique that allows to understand changes in importance of different variables over space (which may indicate that the model used is mis-specified and can be improved).
There are two examples here. One short example with California precipitation data, and than a more elaborate example with house price data.
California precipitation
if (!require("rspat")) remotes::install_github('rspatial/rspat')
## Loading required package: rspat
## Loading required package: terra
## terra 1.8.23
library(rspat)
counties <- spat_data("counties")
p <- spat_data("precipitation")
head(p)
## ID NAME LAT LONG ALT JAN FEB MAR APR MAY JUN JUL
## 1 ID741 DEATH VALLEY 36.47 -116.87 -59 7.4 9.5 7.5 3.4 1.7 1.0 3.7
## 2 ID743 THERMAL/FAA AIRPORT 33.63 -116.17 -34 9.2 6.9 7.9 1.8 1.6 0.4 1.9
## 3 ID744 BRAWLEY 2SW 32.96 -115.55 -31 11.3 8.3 7.6 2.0 0.8 0.1 1.9
## 4 ID753 IMPERIAL/FAA AIRPORT 32.83 -115.57 -18 10.6 7.0 6.1 2.5 0.2 0.0 2.4
## 5 ID754 NILAND 33.28 -115.51 -18 9.0 8.0 9.0 3.0 0.0 1.0 8.0
## 6 ID758 EL CENTRO/NAF 32.82 -115.67 -13 9.8 1.6 3.7 3.0 0.4 0.0 3.0
## AUG SEP OCT NOV DEC
## 1 2.8 4.3 2.2 4.7 3.9
## 2 3.4 5.3 2.0 6.3 5.5
## 3 9.2 6.5 5.0 4.8 9.7
## 4 2.6 8.3 5.4 7.7 7.3
## 5 9.0 7.0 8.0 7.0 9.0
## 6 10.8 0.2 0.0 3.3 1.4
plot(counties)
points(p[,c("LONG", "LAT")], col="red", pch=20)
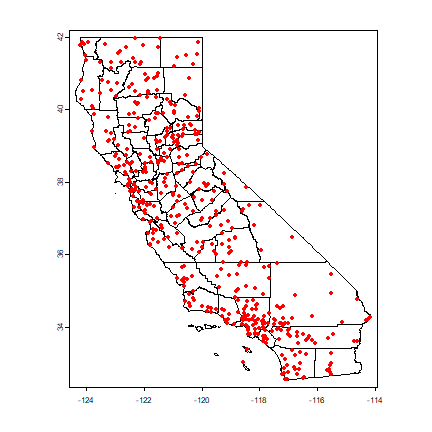
Compute annual average precipitation
p$pan <- rowSums(p[,6:17])
Global regression model
m <- lm(pan ~ ALT, data=p)
m
##
## Call:
## lm(formula = pan ~ ALT, data = p)
##
## Coefficients:
## (Intercept) ALT
## 523.60 0.17
Create a SpatVector objects with a planar crs.
alb <- "+proj=aea +lat_1=34 +lat_2=40.5 +lat_0=0 +lon_0=-120 +x_0=0 +y_0=-4000000 +datum=WGS84 +units=m"
sp <- vect(p, c("LONG", "LAT"), crs="+proj=longlat +datum=WGS84")
spt <- project(sp, alb)
ctst <- project(counties, alb)
Get the optimal bandwidth
library( spgwr )
## Loading required package: sp
## Loading required package: spData
## To access larger datasets in this package, install the spDataLarge
## package with: `install.packages('spDataLarge',
## repos='https://nowosad.github.io/drat/', type='source')`
## NOTE: This package does not constitute approval of GWR
## as a method of spatial analysis; see example(gwr)
bw <- gwr.sel(pan ~ ALT, data=as.data.frame(spt), coords=geom(spt)[,c("x", "y")])
## Bandwidth: 526221.1 CV score: 64886883
## Bandwidth: 850593.6 CV score: 74209073
## Bandwidth: 325747.9 CV score: 54001118
## Bandwidth: 201848.6 CV score: 44611213
## Bandwidth: 125274.7 CV score: 35746320
## Bandwidth: 77949.39 CV score: 29181737
## Bandwidth: 48700.74 CV score: 22737197
## Bandwidth: 30624.09 CV score: 17457161
## Bandwidth: 19452.1 CV score: 15163436
## Bandwidth: 12547.43 CV score: 19452191
## Bandwidth: 22792.75 CV score: 15512988
## Bandwidth: 17052.67 CV score: 15709960
## Bandwidth: 20218.99 CV score: 15167438
## Bandwidth: 19767.99 CV score: 15156913
## Bandwidth: 19790.05 CV score: 15156906
## Bandwidth: 19781.39 CV score: 15156902
## Bandwidth: 19781.48 CV score: 15156902
## Bandwidth: 19781.47 CV score: 15156902
## Bandwidth: 19781.47 CV score: 15156902
## Bandwidth: 19781.47 CV score: 15156902
## Bandwidth: 19781.47 CV score: 15156902
bw
## [1] 19781.47
Create a regular set of points to estimate parameters for.
r <- rast(ctst, res=10000)
r <- rasterize(ctst, r)
newpts <- as.points(r)
Run the gwr function
g <- gwr(pan ~ ALT, data=as.data.frame(spt), coords=geom(spt)[,c("x", "y")], bandwidth=bw, fit.points=geom(newpts)[,c("x", "y")])
g
## Call:
## gwr(formula = pan ~ ALT, data = as.data.frame(spt), coords = geom(spt)[,
## c("x", "y")], bandwidth = bw, fit.points = geom(newpts)[,
## c("x", "y")])
## Kernel function: gwr.Gauss
## Fixed bandwidth: 19781.47
## Fit points: 4090
## Summary of GWR coefficient estimates at fit points:
## Min. 1st Qu. Median 3rd Qu. Max.
## X.Intercept. -846.314308 77.986476 328.579339 729.588996 3452.1972
## ALT -3.961701 0.034149 0.201568 0.418716 4.6022
Link the results back to the raster
slope <- intercept <- r
slope[!is.na(slope)] <- g$SDF$ALT
intercept[!is.na(intercept)] <- g$SDF$'(Intercept)'
s <- c(intercept, slope)
names(s) <- c('intercept', 'slope')
plot(s)
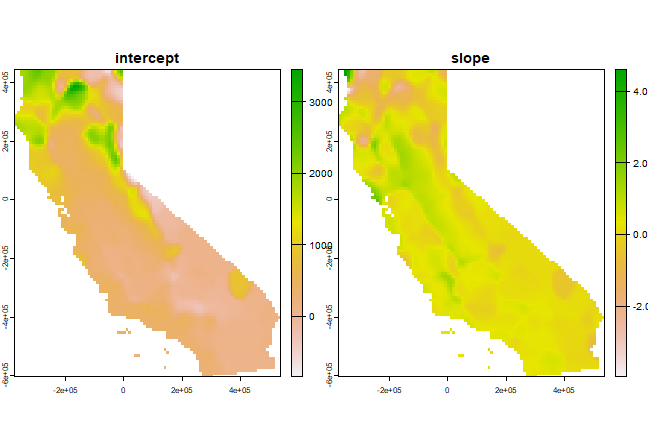
California House Price Data
We will use house prices data from the 1990 census, taken from “Pace, R.K. and R. Barry, 1997. Sparse Spatial Autoregressions. Statistics and Probability Letters 33: 291-297.”
houses <- spat_data("houses1990.csv")
dim(houses)
## [1] 20640 9
head(houses)
## houseValue income houseAge rooms bedrooms population households latitude
## 1 452600 8.3252 41 880 129 322 126 37.88
## 2 358500 8.3014 21 7099 1106 2401 1138 37.86
## 3 352100 7.2574 52 1467 190 496 177 37.85
## 4 341300 5.6431 52 1274 235 558 219 37.85
## 5 342200 3.8462 52 1627 280 565 259 37.85
## 6 269700 4.0368 52 919 213 413 193 37.85
## longitude
## 1 -122.23
## 2 -122.22
## 3 -122.24
## 4 -122.25
## 5 -122.25
## 6 -122.25
Each record represents a census “blockgroup”. The longitude and latitude of the centroids of each block group are available. We can use that to make a map and we can also use these to link the data to other spatial data. For example to get county-membership of each block group. To do that, let’s first turn this into a SpatialPointsDataFrame to find out to which county each point belongs.
hvect <- vect(houses, c("longitude", "latitude"))
plot(hvect, cex=0.5, pch=1, axes=TRUE)
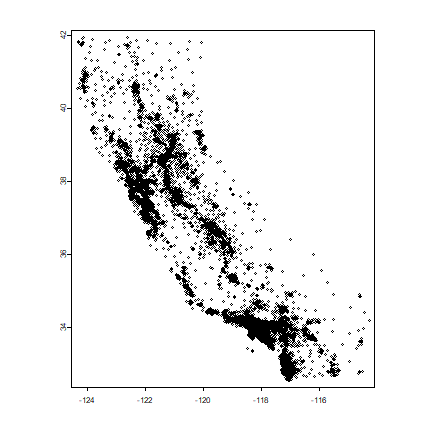
Now get the county boundaries and assign CRS of the houses data matches that of the counties (because they are both in longitude/latitude!).
crs(hvect) <- crs(counties)
Do a spatial query (points in polygon)
cnty <- extract(counties, hvect)
head(cnty)
## id.y STATE COUNTY NAME LSAD LSAD_TRANS
## 1 1 06 001 Alameda 06 County
## 2 2 06 001 Alameda 06 County
## 3 3 06 001 Alameda 06 County
## 4 4 06 001 Alameda 06 County
## 5 5 06 001 Alameda 06 County
## 6 6 06 001 Alameda 06 County
Summarize
We can summarize the data by county. First combine the extracted county data with the original data.
hd <- cbind(data.frame(houses), cnty)
Compute the population by county
totpop <- tapply(hd$population, hd$NAME, sum)
totpop
## Alameda Alpine Amador Butte Calaveras
## 1241779 1113 30039 182120 31998
## Colusa Contra Costa Del Norte El Dorado Fresno
## 16275 799017 16045 128624 662261
## Glenn Humboldt Imperial Inyo Kern
## 24798 116418 108633 18281 528995
## Kings Lake Lassen Los Angeles Madera
## 91842 50631 27214 8721937 88089
## Marin Mariposa Mendocino Merced Modoc
## 204241 14302 75061 176457 9678
## Mono Monterey Napa Nevada Orange
## 9956 342314 108030 78510 2340204
## Placer Plumas Riverside Sacramento San Benito
## 170761 19739 1162787 1038540 36697
## San Bernardino San Diego San Francisco San Joaquin San Luis Obispo
## 1409740 2425153 683068 477184 203764
## San Mateo Santa Barbara Santa Clara Santa Cruz Shasta
## 614816 335177 1486054 216732 147036
## Sierra Siskiyou Solano Sonoma Stanislaus
## 3318 43531 337429 385296 370821
## Sutter Tehama Trinity Tulare Tuolumne
## 63689 49625 13063 309073 48456
## Ventura Yolo Yuba
## 649935 138799 58954
Income is harder because we have the median household income by blockgroup. But it can be approximated by first computing total income by blockgroup, summing that, and dividing that by the total number of households.
# total income
hd$suminc <- hd$income * hd$households
# now use aggregate (similar to tapply)
csum <- aggregate(hd[, c('suminc', 'households')], list(hd$NAME), sum)
# divide total income by number of housefholds
csum$income <- 10000 * csum$suminc / csum$households
# sort
csum <- csum[order(csum$income), ]
head(csum)
## Group.1 suminc households income
## 53 Trinity 11198.985 5156 21720.30
## 58 Yuba 43739.708 19882 21999.65
## 25 Modoc 8260.597 3711 22259.76
## 47 Siskiyou 38769.952 17302 22407.79
## 17 Lake 47612.899 20805 22885.32
## 11 Glenn 20497.683 8821 23237.37
tail(csum)
## Group.1 suminc households income
## 56 Ventura 994094.8 210418 47243.81
## 7 Contra Costa 1441734.6 299123 48198.72
## 30 Orange 3938638.1 800968 49173.48
## 43 Santa Clara 2621895.6 518634 50553.87
## 41 San Mateo 1169145.6 230674 50683.89
## 21 Marin 436808.4 85869 50869.17
Regression
Before we make a regression model, let’s first add some new variables that we might use, and then see if we can build a regression model with house price as dependent variable. The authors of the paper used a lot of log tranforms, so you can also try that.
hd$roomhead <- hd$rooms / hd$population
hd$bedroomhead <- hd$bedrooms / hd$population
hd$hhsize <- hd$population / hd$households
Ordinary least squares regression:
# OLS
m <- glm( houseValue ~ income + houseAge + roomhead + bedroomhead + population, data=hd)
summary(m)
##
## Call:
## glm(formula = houseValue ~ income + houseAge + roomhead + bedroomhead +
## population, data = hd)
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -6.508e+04 2.533e+03 -25.686 < 2e-16 ***
## income 5.179e+04 3.833e+02 135.092 < 2e-16 ***
## houseAge 1.832e+03 4.575e+01 40.039 < 2e-16 ***
## roomhead -4.720e+04 1.489e+03 -31.688 < 2e-16 ***
## bedroomhead 2.648e+05 6.820e+03 38.823 < 2e-16 ***
## population 3.947e+00 5.081e-01 7.769 8.27e-15 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for gaussian family taken to be 6022427437)
##
## Null deviance: 2.7483e+14 on 20639 degrees of freedom
## Residual deviance: 1.2427e+14 on 20634 degrees of freedom
## AIC: 523369
##
## Number of Fisher Scoring iterations: 2
coefficients(m)
## (Intercept) income houseAge roomhead bedroomhead
## -65075.701407 51786.005862 1831.685266 -47198.908765 264766.186284
## population
## 3.947461
Geographicaly Weighted Regression
By county
Of course we could make the model more complex, with e.g. squared income, and interactions. But let’s see if we can do Geographically Weighted regression. One approach could be to use counties.
First I remove records that were outside the county boundaries
hd2 <- hd[!is.na(hd$NAME), ]
Then I write a function to get what I want from the regression (the coefficients in this case)
regfun <- function(x) {
dat <- hd2[hd2$NAME == x, ]
m <- glm(houseValue~income+houseAge+roomhead+bedroomhead+population, data=dat)
coefficients(m)
}
And now run this for all counties using sapply:
countynames <- unique(hd2$NAME)
res <- sapply(countynames, regfun)
Plot of a single coefficient
dotchart(sort(res["income", ]), cex=0.65)

There clearly is variation in the coefficient (\(beta\)) for income. How does this look on a map?
First make a data.frame of the results
resdf <- data.frame(NAME=colnames(res), t(res))
head(resdf)
## NAME X.Intercept. income houseAge roomhead
## Alameda Alameda -62373.62 35842.330 591.1001 24147.3182
## Contra Costa Contra Costa -61759.84 43668.442 465.8897 -356.6085
## Alpine Alpine -77605.93 40850.588 5595.4113 NA
## Amador Amador 120480.71 3234.519 -771.5857 37997.0069
## Butte Butte 50935.36 15577.745 -380.5824 9078.9315
## Calaveras Calaveras 91364.72 7126.668 -929.4065 16843.3456
## bedroomhead population
## Alameda 129814.33 8.0570859
## Contra Costa 150662.89 0.8869663
## Alpine NA NA
## Amador -194176.65 0.9971630
## Butte -32272.68 5.7707597
## Calaveras -78749.86 8.8865713
Fix the counties object. There are too many counties because of the presence of islands. I first aggregate (‘dissolve’ in GIS-speak’) the counties such that a single county becomes a single (multi-)polygon.
dim(counties)
## [1] 68 5
dcounties <- aggregate(counties[, "NAME"], "NAME")
dim(dcounties)
## [1] 58 2
Now we can merge this SpatVector with the data.frame with the regression results.
cnres <- merge(dcounties, resdf, by="NAME")
plot(cnres, "income")

To show all parameters in a ‘conditioning plot’, we need to first scale the values to get similar ranges.
# a copy of the data
cnres2 <- cnres
# scale all variables, except the first one (county name)
values(cnres2) <- as.data.frame(scale(as.data.frame(cnres)[,-1]))
plot(cnres2, names(cnres2)[1:6], plg=list(x="topright"), mar=c(1,1,1,1))
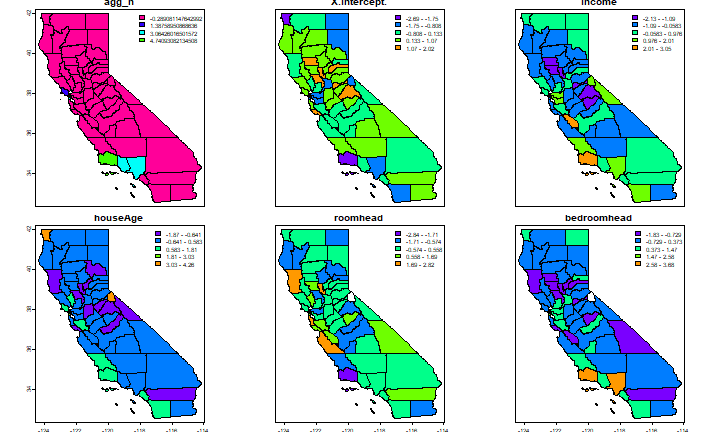
Is this just random noise, or is there spatial autocorrelation?
lw <- adjacent(cnres2, pairs=FALSE)
autocor(cnres$income, lw)
## [1] 0.1565227
autocor(cnres$houseAge, lw)
## [1] -0.02057022
By grid cell
An alternative approach would be to compute a model for grid cells. Let’s use the ‘Teale Albers’ projection (often used when mapping the entire state of California).
TA <- "+proj=aea +lat_1=34 +lat_2=40.5 +lat_0=0 +lon_0=-120 +x_0=0 +y_0=-4000000 +datum=WGS84 +units=m"
countiesTA <- project(counties, TA)
Create a SpatRaster using the extent of the counties, and setting an arbitrary resolution of 50 by 50 km cells
r <- rast(countiesTA)
res(r) <- 50000
Get the xy coordinates for each raster cell:
xy <- xyFromCell(r, 1:ncell(r))
For each cell, we need to select a number of observations, let’s say within 50 km of the center of each cell (thus the data that are used in different cells overlap). And let’s require at least 50 observations to do a regression.
First transform the houses data to Teale-Albers
housesTA <- project(hvect, TA)
crds <- geom(housesTA)[, c("x", "y")]
Set up a new regression function.
regfun2 <- function(d) {
m <- glm(houseValue~income+houseAge+roomhead+bedroomhead+population, data=d)
coefficients(m)
}
Run the model for al cells if there are at least 50 observations within a radius of 50 km.
res <- list()
for (i in 1:nrow(xy)) {
d <- sqrt((xy[i,1]-crds[,1])^2 + (xy[i,2]-crds[,2])^2)
j <- which(d < 50000)
if (length(j) > 49) {
d <- hd[j,]
res[[i]] <- regfun2(d)
} else {
res[[i]] <- NA
}
}
For each cell get the income coefficient:
inc <- sapply(res, function(x) x['income'])
Use these values in a SpatRaster
rinc <- setValues(r, inc)
plot(rinc)
plot(countiesTA, add=T)
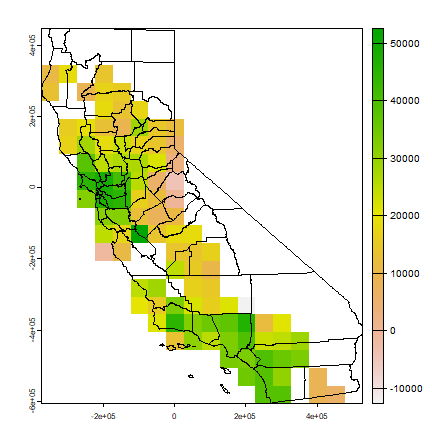
autocor(rinc)
## lyr.1
## 0.4452912
So that was a lot of ‘home-brew-GWR’.
Question 1: Can you comment on weaknesses (and perhaps strengths) of the approaches I have shown?
spgwr package
Now use the spgwr package (and the the gwr function) to fit the
model. You can do this with all data, as long as you supply and argument
fit.points (to avoid estimating a model for each observation point.
You can use a raster similar to the one I used above (perhaps
disaggregate with a factor 2 first).
This is how you can get the points to use:
Create a SpatRaster with the correct extent
r <- rast(countiesTA)
Set to a desired resolution. I choose 25 km
res(r) <- 25000
I only want cells inside of CA, so I add some more steps.
ca <- rasterize(countiesTA, r)
Extract the coordinates that are not NA.
fitpoints <- crds(ca)
Now specify the model
gwr.model <- ______
gwr returns a list-like object that includes (as first element) a
SpatialPointsDataFrame that has the model coefficients. Plot these
and, after that, transfer them to a SpatRaster.
To extract the SpatialPointsDataFrame:
sp <- gwr.model$SDF
v <- vect(sp)
v
To reconnect these values to the raster structure (etc.)
cells <- cellFromXY(r, fitpoints)
dd <- as.matrix(data.frame(sp))
b <- rast(r, nl=ncol(dd))
b[cells] <- dd
names(b) <- colnames(dd)
plot(b)
Question 2: spgwr shows a remarkable startup message. What is that about?
Question 3: Briefly comment on the results and the differences (if any) with the two home-brew examples.