Interpolation

Introduction

Almost any variable of interest has spatial autocorrelation. That can be a problem in statistical tests, but it is a very useful feature when we want to predict values at locations where no measurements have been made; as we can generally safely assume that values at nearby locations will be similar. There are several spatial interpolation techniques. We show some of them in this chapter.

Temperature in California

We will be working with temperature data for California. If have not yet done so, first install the rspatial package to get the data. You may need to install the devtools package first.

if (!require("rspatial")) remotes::install_github('rspatial/rspatial')
## Loading required package: rspatial

Now get the data

library(rspatial)
d <- sp_data('precipitation')
head(d)
##      ID                 NAME   LAT    LONG ALT  JAN FEB MAR APR MAY JUN JUL
## 1 ID741         DEATH VALLEY 36.47 -116.87 -59  7.4 9.5 7.5 3.4 1.7 1.0 3.7
## 2 ID743  THERMAL/FAA AIRPORT 33.63 -116.17 -34  9.2 6.9 7.9 1.8 1.6 0.4 1.9
## 3 ID744          BRAWLEY 2SW 32.96 -115.55 -31 11.3 8.3 7.6 2.0 0.8 0.1 1.9
## 4 ID753 IMPERIAL/FAA AIRPORT 32.83 -115.57 -18 10.6 7.0 6.1 2.5 0.2 0.0 2.4
## 5 ID754               NILAND 33.28 -115.51 -18  9.0 8.0 9.0 3.0 0.0 1.0 8.0
## 6 ID758        EL CENTRO/NAF 32.82 -115.67 -13  9.8 1.6 3.7 3.0 0.4 0.0 3.0
##    AUG SEP OCT NOV DEC
## 1  2.8 4.3 2.2 4.7 3.9
## 2  3.4 5.3 2.0 6.3 5.5
## 3  9.2 6.5 5.0 4.8 9.7
## 4  2.6 8.3 5.4 7.7 7.3
## 5  9.0 7.0 8.0 7.0 9.0
## 6 10.8 0.2 0.0 3.3 1.4

Compute annual precipitation

d$prec <- rowSums(d[, c(6:17)])
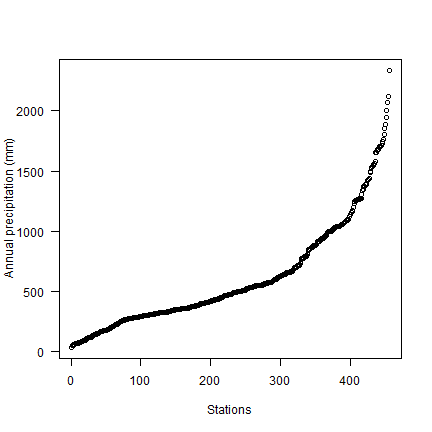
plot(sort(d$prec), ylab='Annual precipitation (mm)', las=1, xlab='Stations')

Now make a quick map.

library(sp)
dsp <- SpatialPoints(d[,4:3], proj4string=CRS("+proj=longlat +datum=NAD83"))
dsp <- SpatialPointsDataFrame(dsp, d)
CA <- sp_data("counties")
# define groups for mapping
cuts <- c(0,200,300,500,1000,3000)
# set up a palette of interpolated colors
blues <- colorRampPalette(c('yellow', 'orange', 'blue', 'dark blue'))
pols <- list("sp.polygons", CA, fill = "lightgray")
spplot(dsp, 'prec', cuts=cuts, col.regions=blues(5), sp.layout=pols, pch=20, cex=2)

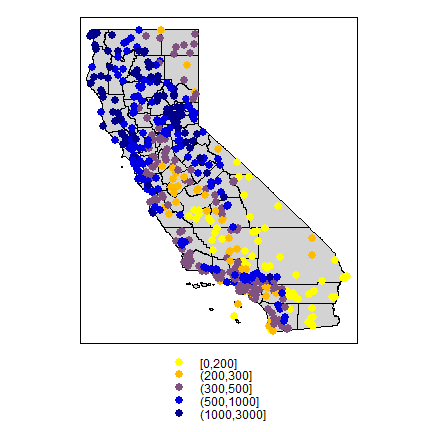
Transform longitude/latitude to planar coordinates, using the commonly used coordinate reference system for California (“Teale Albers”) to assure that our interpolation results will align with other data sets we have.

TA <- CRS("+proj=aea +lat_1=34 +lat_2=40.5 +lat_0=0 +lon_0=-120 +x_0=0 +y_0=-4000000 +datum=WGS84 +units=m")
library(rgdal)
dta <- spTransform(dsp, TA)
cata <- spTransform(CA, TA)

9.2 NULL model

We are going to interpolate (estimate for unsampled locations) the precipitation values. The simplest way would be to take the mean of all observations. We can consider that a “Null-model” that we can compare other approaches to. We’ll use the Root Mean Square Error (RMSE) as evaluation statistic.

RMSE <- function(observed, predicted) {
  sqrt(mean((predicted - observed)^2, na.rm=TRUE))
}

Get the RMSE for the Null-model

null <- RMSE(mean(dsp$prec), dsp$prec)
null
## [1] 435.3217

proximity polygons

Proximity polygons can be used to interpolate categorical variables. Another term for this is “nearest neighbour” interpolation.

library(dismo)
v <- voronoi(dta)
plot(v)

Looks weird. Let’s confine this to California

ca <- aggregate(cata)
vca <- intersect(v, ca)
spplot(vca, 'prec', col.regions=rev(get_col_regions()))

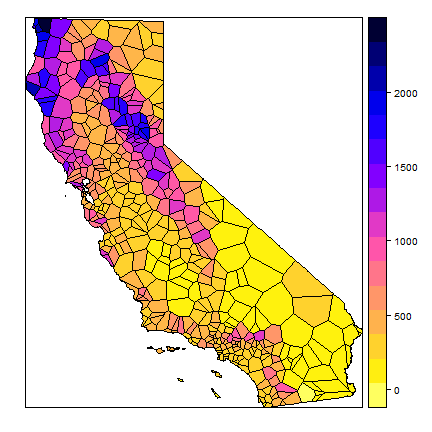
Much better. These are polygons. We can ‘rasterize’ the results like this.

r <- raster(cata, res=10000)
vr <- rasterize(vca, r, 'prec')
plot(vr)

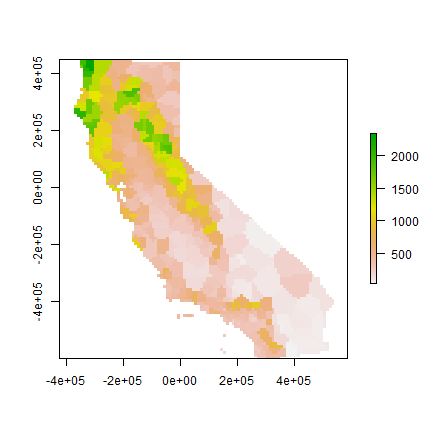
Now evaluate with 5-fold cross validation.

set.seed(5132015)
kf <- kfold(nrow(dta))
rmse <- rep(NA, 5)
for (k in 1:5) {
  test <- dta[kf == k, ]
  train <- dta[kf != k, ]
  v <- voronoi(train)
  p <- extract(v, test)
  rmse[k] <- RMSE(test$prec, p$prec)
}
rmse
## [1] 199.0686 187.8069 166.9153 197.8713 238.9696
mean(rmse)
## [1] 198.1263
1 - (mean(rmse) / null)
## [1] 0.5448738

Question 1: Describe what each step in the code chunk above does

Question 2: How does the proximity-polygon approach compare to the NULL model?

Question 3: You would not typically use proximty polygons for rainfall data. For what kind of data would you use them?

Nearest neighbour interpolation

Here we do nearest neighbour interpolation considering multiple (5) neighbours.

We can use the gstat package for this. First we fit a model. ~1 means “intercept only”. In the case of spatial data, that would be only ‘x’ and ‘y’ coordinates are used. We set the maximum number of points to 5, and the “inverse distance power” idp to zero, such that all five neighbors are equally weighted

library(gstat)
gs <- gstat(formula=prec~1, locations=dta, nmax=5, set=list(idp = 0))
nn <- interpolate(r, gs)
## [inverse distance weighted interpolation]
nnmsk <- mask(nn, vr)
plot(nnmsk)

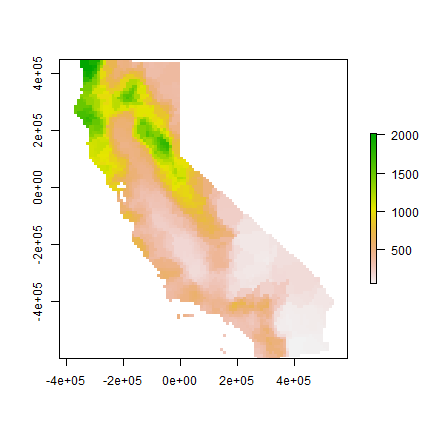
Cross validate the result. Note that we can use the predict method to get predictions for the locations of the test points.

rmsenn <- rep(NA, 5)
for (k in 1:5) {
  test <- dta[kf == k, ]
  train <- dta[kf != k, ]
  gscv <- gstat(formula=prec~1, locations=train, nmax=5, set=list(idp = 0))
  p <- predict(gscv, test)$var1.pred
  rmsenn[k] <- RMSE(test$prec, p)
}
## [inverse distance weighted interpolation]
## [inverse distance weighted interpolation]
## [inverse distance weighted interpolation]
## [inverse distance weighted interpolation]
## [inverse distance weighted interpolation]
rmsenn
## [1] 200.6222 190.8336 180.3833 169.9658 237.9067
mean(rmsenn)
## [1] 195.9423
1 - (mean(rmsenn) / null)
## [1] 0.5498908

Inverse distance weighted

A more commonly used method is “inverse distance weighted” interpolation. The only difference with the nearest neighbour approach is that points that are further away get less weight in predicting a value a location.

library(gstat)
gs <- gstat(formula=prec~1, locations=dta)
idw <- interpolate(r, gs)
## [inverse distance weighted interpolation]
idwr <- mask(idw, vr)
plot(idwr)

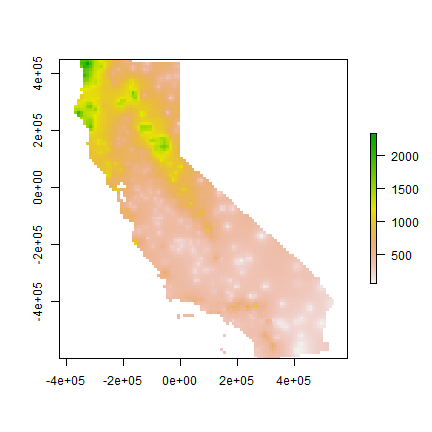
Question 4: IDW generated rasters tend to have a noticeable artefact. What is that?

Cross validate. We can predict to the locations of the test points

rmse <- rep(NA, 5)
for (k in 1:5) {
  test <- dta[kf == k, ]
  train <- dta[kf != k, ]
  gs <- gstat(formula=prec~1, locations=train)
  p <- predict(gs, test)
  rmse[k] <- RMSE(test$prec, p$var1.pred)
}
## [inverse distance weighted interpolation]
## [inverse distance weighted interpolation]
## [inverse distance weighted interpolation]
## [inverse distance weighted interpolation]
## [inverse distance weighted interpolation]
rmse
## [1] 215.3319 211.9383 190.0231 211.8308 230.1893
mean(rmse)
## [1] 211.8627
1 - (mean(rmse) / null)
## [1] 0.5133192

Question 5: Inspect the arguments used for and make a map of the IDW model below. What other name could you give to this method (IDW with these parameters)? Why?

gs2 <- gstat(formula=prec~1, locations=dta, nmax=1, set=list(idp=1))

Calfornia Air Pollution data

We use California Air Pollution data to illustrate geostatistcal (Kriging) interpolation.

Data preparation

We use the airqual dataset to interpolate ozone levels for California (averages for 1980-2009). Use the variable OZDLYAV (unit is parts per billion). Original data source.

Read the data file. To get easier numbers to read, I multiply OZDLYAV with 1000

x <- sp_data("airqual")
x$OZDLYAV <- x$OZDLYAV * 1000

Create a SpatialPointsDataFrame and transform to Teale Albers. Note the units=km, which was needed to fit the variogram.

coordinates(x) <- ~LONGITUDE + LATITUDE
proj4string(x) <- CRS('+proj=longlat +datum=NAD83')
TA <- CRS("+proj=aea +lat_1=34 +lat_2=40.5 +lat_0=0 +lon_0=-120 +x_0=0 +y_0=-4000000 +datum=WGS84 +units=km")
library(rgdal)
aq <- spTransform(x, TA)

Create an template raster to interpolate to. E.g., given a SpatialPolygonsDataFrame of California, ‘ca’. Coerce that to a ‘SpatialGrid’ object (a different representation of the same idea)

cageo <- sp_data('counties.rds')
ca <- spTransform(cageo, TA)
r <- raster(ca)
res(r) <- 10  # 10 km if your CRS's units are in km
g <- as(r, 'SpatialGrid')

Fit a variogram

Use gstat to create an emperical variogram ‘v’

library(gstat)
gs <- gstat(formula=OZDLYAV~1, locations=aq)
v <- variogram(gs, width=20)
head(v)
##     np      dist    gamma dir.hor dir.ver   id
## 1 1010  11.35040 34.80579       0       0 var1
## 2 1806  30.63737 47.52591       0       0 var1
## 3 2355  50.58656 67.26548       0       0 var1
## 4 2619  70.10411 80.92707       0       0 var1
## 5 2967  90.13917 88.93653       0       0 var1
## 6 3437 110.42302 84.13589       0       0 var1
plot(v)

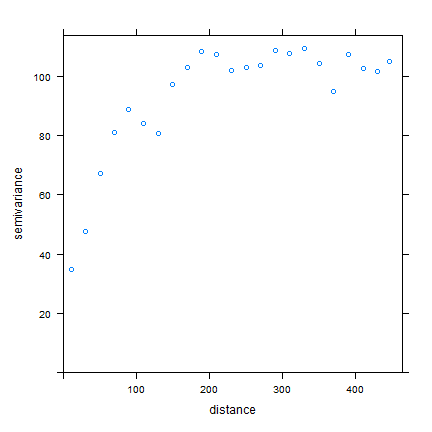
Now, fit a model variogram

fve <- fit.variogram(v, vgm(85, "Exp", 75, 20))
fve
##   model    psill    range
## 1   Nug 21.96600  0.00000
## 2   Exp 85.52957 72.31404
plot(variogramLine(fve, 400), type='l', ylim=c(0,120))
points(v[,2:3], pch=20, col='red')

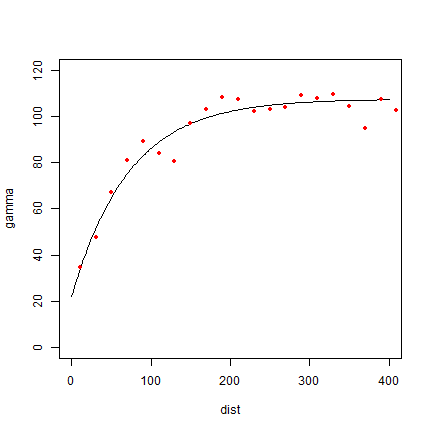
Try a different type (spherical in stead of exponential)

fvs <- fit.variogram(v, vgm(85, "Sph", 75, 20))
fvs
##   model    psill    range
## 1   Nug 25.57019   0.0000
## 2   Sph 72.65881 135.7744
plot(variogramLine(fvs, 400), type='l', ylim=c(0,120) ,col='blue', lwd=2)
points(v[,2:3], pch=20, col='red')

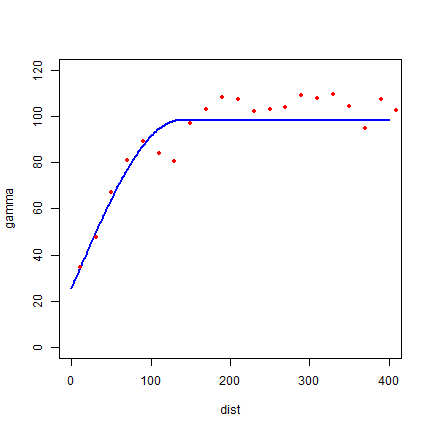
Both look pretty good in this case.

Another way to plot the variogram and the model

plot(v, fve)

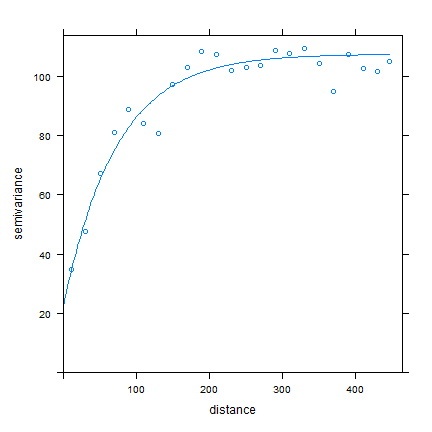
Ordinary kriging

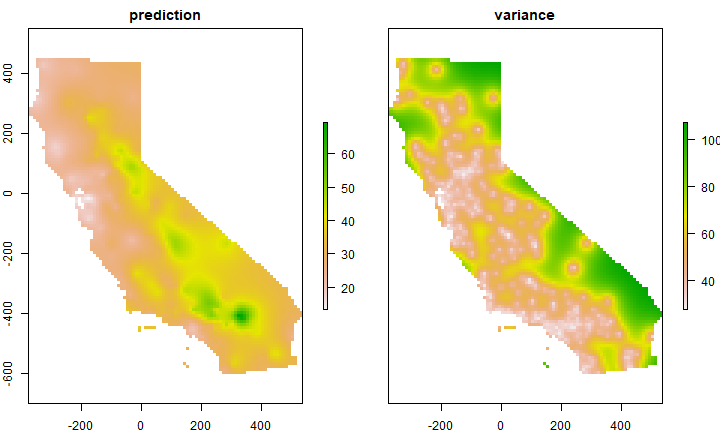
Use variogram fve in a kriging interpolation

k <- gstat(formula=OZDLYAV~1, locations=aq, model=fve)
# predicted values
kp <- predict(k, g)
## [using ordinary kriging]
spplot(kp)

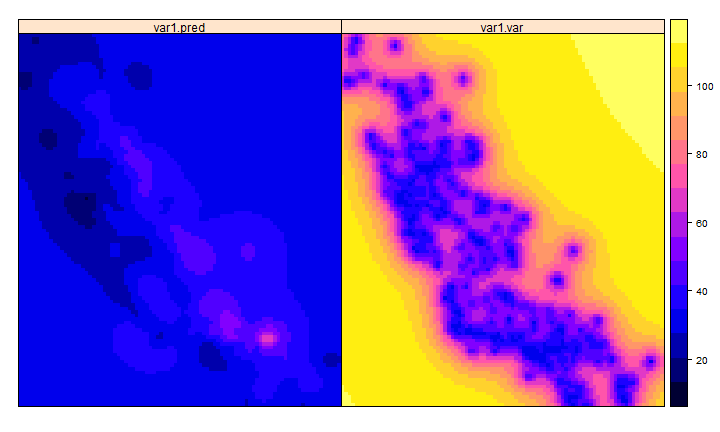
# variance
ok <- brick(kp)
ok <- mask(ok, ca)
names(ok) <- c('prediction', 'variance')
plot(ok)

Compare with other methods

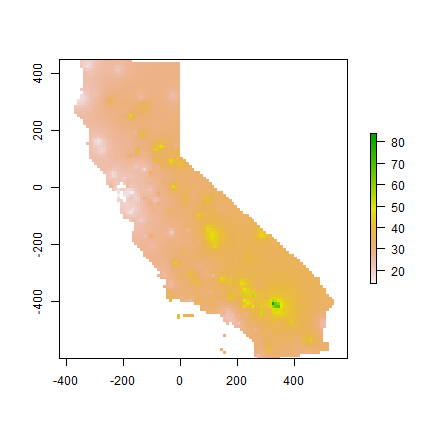
Let’s use gstat again to do IDW interpolation. The basic approach first.

library(gstat)
idm <- gstat(formula=OZDLYAV~1, locations=aq)
idp <- interpolate(r, idm)
## [inverse distance weighted interpolation]
idp <- mask(idp, ca)
plot(idp)

We can find good values for the idw parameters (distance decay and number of neighbours) through optimization. For simplicity’s sake I do not do that k times here. The optim function may be a bit hard to grasp at first. But the essence is simple. You provide a function that returns a value that you want to minimize (or maximize) given a number of unknown parameters. Your provide initial values for these parameters, and optim then searches for the optimal values (for which the function returns the lowest number).

RMSE <- function(observed, predicted) {
  sqrt(mean((predicted - observed)^2, na.rm=TRUE))
}
f1 <- function(x, test, train) {
  nmx <- x[1]
  idp <- x[2]
  if (nmx < 1) return(Inf)
  if (idp < .001) return(Inf)
  m <- gstat(formula=OZDLYAV~1, locations=train, nmax=nmx, set=list(idp=idp))
  p <- predict(m, newdata=test, debug.level=0)$var1.pred
  RMSE(test$OZDLYAV, p)
}
set.seed(20150518)
i <- sample(nrow(aq), 0.2 * nrow(aq))
tst <- aq[i,]
trn <- aq[-i,]
opt <- optim(c(8, .5), f1, test=tst, train=trn)
opt
## $par
## [1] 9.2594442 0.6817524
##
## $value
## [1] 7.861426
##
## $counts
## function gradient
##       35       NA
##
## $convergence
## [1] 0
##
## $message
## NULL

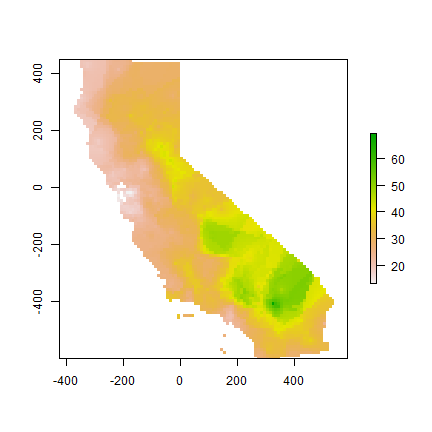
Our optimal IDW model

m <- gstat(formula=OZDLYAV~1, locations=aq, nmax=opt$par[1], set=list(idp=opt$par[2]))
idw <- interpolate(r, m)
## [inverse distance weighted interpolation]
idw <- mask(idw, ca)
plot(idw)

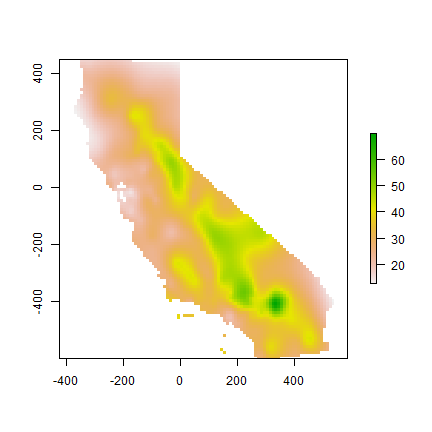
A thin plate spline model

library(fields)
m <- Tps(coordinates(aq), aq$OZDLYAV)
tps <- interpolate(r, m)
tps <- mask(tps, idw)
plot(tps)

Cross-validate

Cross-validate the three methods (IDW, Ordinary kriging, TPS) and add RMSE weighted ensemble model.

library(dismo)
nfolds <- 5
k <- kfold(aq, nfolds)
ensrmse <- tpsrmse <- krigrmse <- idwrmse <- rep(NA, 5)
for (i in 1:nfolds) {
  test <- aq[k!=i,]
  train <- aq[k==i,]
  m <- gstat(formula=OZDLYAV~1, locations=train, nmax=opt$par[1], set=list(idp=opt$par[2]))
  p1 <- predict(m, newdata=test, debug.level=0)$var1.pred
  idwrmse[i] <-  RMSE(test$OZDLYAV, p1)
  m <- gstat(formula=OZDLYAV~1, locations=train, model=fve)
  p2 <- predict(m, newdata=test, debug.level=0)$var1.pred
  krigrmse[i] <-  RMSE(test$OZDLYAV, p2)
  m <- Tps(coordinates(train), train$OZDLYAV)
  p3 <- predict(m, coordinates(test))
  tpsrmse[i] <-  RMSE(test$OZDLYAV, p3)
  w <- c(idwrmse[i], krigrmse[i], tpsrmse[i])
  weights <- w / sum(w)
  ensemble <- p1 * weights[1] + p2 * weights[2] + p3 * weights[3]
  ensrmse[i] <-  RMSE(test$OZDLYAV, ensemble)
}
rmi <- mean(idwrmse)
rmk <- mean(krigrmse)
rmt <- mean(tpsrmse)
rms <- c(rmi, rmt, rmk)
rms
## [1] 8.041305 8.307235 7.930799
rme <- mean(ensrmse)
rme
## [1] 7.858051

Question 6: Which method performed best?

We can use the RMSE values to make a weighted ensemble. I use the inverse of the differnce between a model’s RMSE and a NULL model.

nullrmse <- RMSE(test$OZDLYAV, mean(test$OZDLYAV))
w <- 1 / (nullrmse - rms)
weights <- ( w / sum(w) )
# check
sum(weights)
## [1] 1
s <- stack(idw, ok[[1]], tps)
ensemble <- sum(s * weights)

And compare maps.

s <- stack(idw, ok[[1]], tps, ensemble)
names(s) <- c('IDW', 'OK', 'TPS', 'Ensemble')
plot(s)

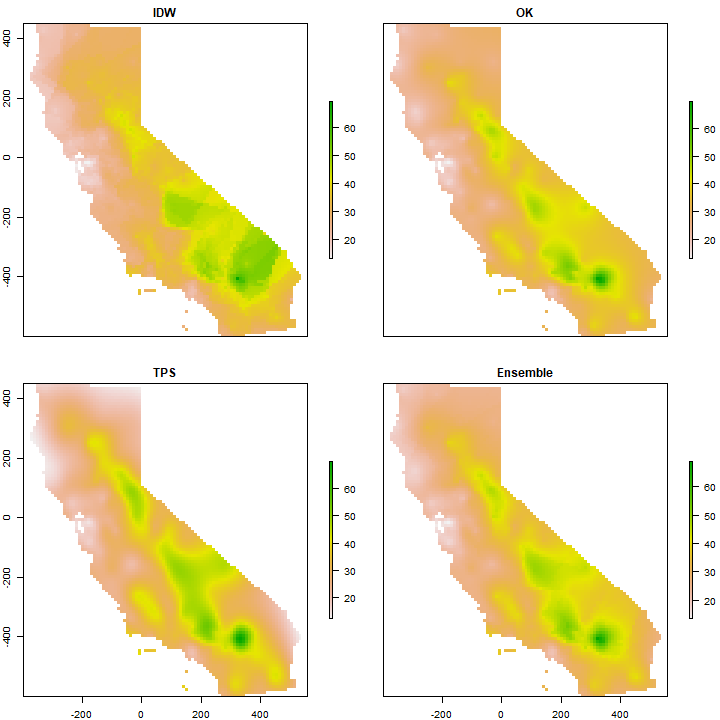
Question 7: Show where the largest difference exist between IDW and OK.

Question 8: Show where the difference between IDW and OK is within the 95% confidence limit of the OK prediction.

Question 9: Can you describe the pattern we are seeing, and speculate about what is causing it?