Basic mathematical operations
The terra package supports many mathematical operations. Math
operations are generally performed per pixel (grid cell). First we will
do some basic arithmetic operations to combine bands. In the first
example we write a custom math function to calculate the Normalized
Difference Vegetation Index (NDVI). Learn more about vegetation indices
here
and NDVI.
We use the same Landsat data as in Chapter 2.
library(terra)
## terra 1.8.23
rfiles <- paste0('data/rs/LC08_044034_20170614_B', 1:11, ".tif")
landsat <- rast(rfiles)
landsatRGB <- landsat[[c(4,3,2)]]
landsatFCC <- landsat[[c(5,4,3)]]
Vegetation indices
Let’s define a general function for a ratio based (vegetation) index. In
the function below, img is a muti-layer SpatRaster object and i
and k are the indices of the layers (layer numbers) used to compute
the vegetation index.
vi <- function(img, k, i) {
bk <- img[[k]]
bi <- img[[i]]
vi <- (bk - bi) / (bk + bi)
return(vi)
}
# For Landsat NIR = 5, red = 4.
ndvi <- vi(landsat, 5, 4)
plot(ndvi, col=rev(terrain.colors(10)), main = "NDVI")
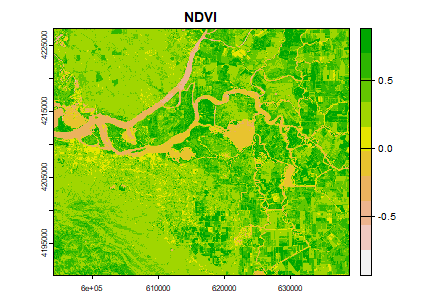
You can see the variation in greenness from the plot.
Below is an alternative way to accomplish this. First write a general function that can compute 2-layer NDVI type indices.
vi2 <- function(x, y) {
(x - y) / (x + y)
}
And use that function as an argument in lapp
nir <- landsat[[5]]
red <- landsat[[4]]
ndvi2 <- lapp(c(nir, red), fun = vi2)
# or in one line
#ndvi2 <- lapp(landsat[[5:4]], fun=vi2)
plot(ndvi2, col=rev(terrain.colors(10)), main="Landsat-NDVI")
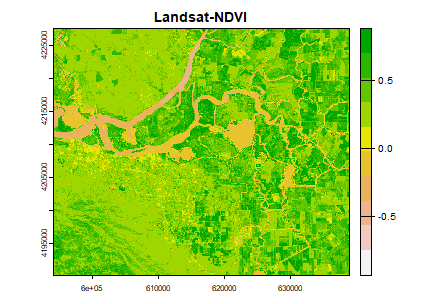
Question 1: Adapt the code shown above to compute indices to identify i) water and ii) built-up. Hint: Use the spectral profile plot to find the bands having maximum and minimum reflectance for these two classes. Or read about it here..
Histogram
We can explore the distribution of values contained within our raster
using hist to produces a histogram. Histograms are often useful in
identifying outliers and bad data values in our raster data.
hist(ndvi, main = "NDVI values", xlab = "NDVI", ylab= "Frequency",
col = "wheat", xlim = c(-0.5, 1), breaks = 30, xaxt = "n")
## Warning: [hist] a sample of 54% of the cells was used
axis(side=1, at = seq(-0.6, 1, 0.2), labels = seq(-0.6, 1, 0.2))
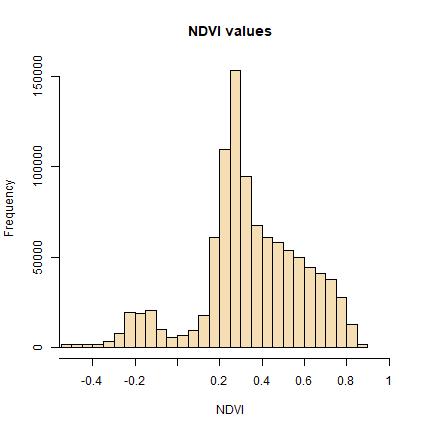
We will refer to this histogram for the following sub-section on thresholding.
Question 2: Make histograms of the values the vegetation indices developed in question 1.
Thresholding
We can apply basic rules to get an estimate of spatial extent of different Earth surface features. Note that NDVI values are standardized and ranges between -1 to +1. Higher values indicate more green cover.
Cells with NDVI values greater than 0.4 are definitely vegetation. The following operation masks all cells that are perhaps not vegetation (NDVI < 0.4).
veg <- clamp(ndvi, 0.4, values=FALSE)
plot(veg, main='Vegetation')
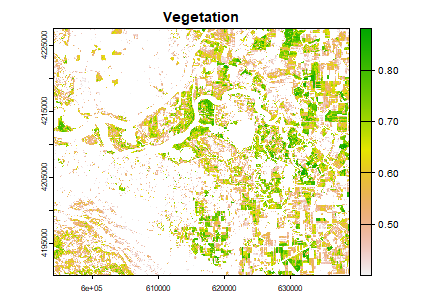
Let’s map the area that corresponds to the peak between 0.25 and 0.3 in the NDVI histogram.
m <- c(-Inf, 0.25, NA, 0.25, 0.3, 1, 0.3, Inf, NA)
rcl <- matrix(m, ncol = 3, byrow = TRUE)
land <- classify(ndvi, rcl)
plot(land, main = 'What is it?')
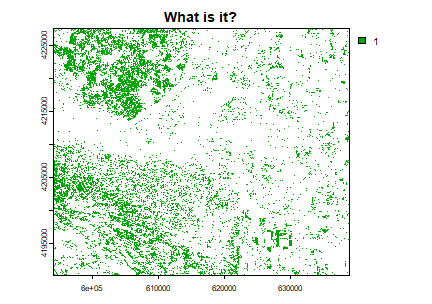
You can plot land on top of the landsatRGB raster to find out.
plotRGB(landsatRGB, r=1, g=2, b=3, axes=TRUE, stretch="lin")
plot(land, add=TRUE, legend=FALSE)

You can also create classes for different intensity of vegetation.
m <- c(-1,0.25, 0.3, 0.4, 0.5, 1)
vegc <- classify(ndvi, m)
plot(vegc, col = rev(terrain.colors(4)), main = 'NDVI based thresholding')
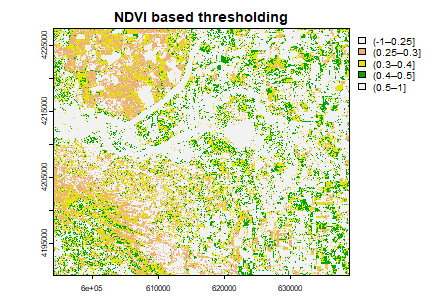
Question 3: Is it possible to find water using thresholding of NDVI or any other indices?
Principal component analysis
Multi-spectral data are sometimes transformed to helps to reduce the dimensionality and noise in the data. The principal components transform is a generic data reduction method that can be used to create a few uncorrelated bands from a larger set of correlated bands.
You can calculate the same number of principal components as the number of input bands. The first principal component (PC) explains the largest percentage of variance and other PCs explain additional the variance in decreasing order.
set.seed(1)
sr <- spatSample(landsat, 10000)
plot(sr[,c(4,5)], main = "NIR-Red plot")
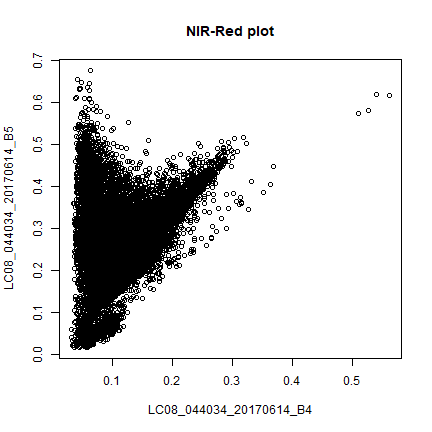
This is known as vegetation and soil-line plot (Same as the scatter plot in earlier section).
pca <- prcomp(sr, scale = TRUE)
pca
## Standard deviations (1, .., p=11):
## [1] 2.53668771 1.40078059 1.08362915 0.92501695 0.54958227 0.41473655
## [7] 0.27030406 0.12220817 0.08661844 0.04763013 0.03609876
##
## Rotation (n x k) = (11 x 11):
## PC1 PC2 PC3 PC4
## LC08_044034_20170614_B1 0.2937880 0.3642123 -0.28481332 -0.06676012
## LC08_044034_20170614_B2 0.3357803 0.3382035 -0.15857739 -0.03635911
## LC08_044034_20170614_B3 0.3612145 0.2650391 0.07275822 0.04141597
## LC08_044034_20170614_B4 0.3676650 0.1641879 0.10447910 0.03578747
## LC08_044034_20170614_B5 0.1591361 -0.1852694 0.71300561 0.32594984
## LC08_044034_20170614_B6 0.3472817 -0.2134275 0.22853576 0.15831890
## LC08_044034_20170614_B7 0.3499019 -0.2367876 -0.11725588 0.06147126
## LC08_044034_20170614_B8 0.3496278 0.1964745 0.08489385 0.02433066
## LC08_044034_20170614_B9 0.1325628 -0.1117693 0.33293128 -0.92447725
## LC08_044034_20170614_B10 0.2534434 -0.4831768 -0.30276292 -0.02013211
## LC08_044034_20170614_B11 0.2507597 -0.4850418 -0.30570381 -0.02197088
## PC5 PC6 PC7 PC8
## LC08_044034_20170614_B1 -0.49633695 -0.17556592 -0.23610914 0.219084848
## LC08_044034_20170614_B2 -0.22593198 -0.09672106 0.06516109 0.191800572
## LC08_044034_20170614_B3 -0.06775249 0.01134076 0.29589321 -0.502516608
## LC08_044034_20170614_B4 0.33203379 0.06966965 0.60728435 0.005032259
## LC08_044034_20170614_B5 -0.51515049 0.06796061 -0.07734807 -0.094468368
## LC08_044034_20170614_B6 0.28840709 -0.33603872 -0.01251499 0.639691364
## LC08_044034_20170614_B7 0.24635064 -0.53401272 -0.39446741 -0.489769588
## LC08_044034_20170614_B8 0.33312920 0.65599341 -0.53808102 0.022845490
## LC08_044034_20170614_B9 -0.04429935 -0.04329372 -0.02425017 -0.001980250
## LC08_044034_20170614_B10 -0.16429483 0.24521079 0.13682816 0.057604000
## LC08_044034_20170614_B11 -0.19644322 0.24453814 0.11434312 -0.028609160
## PC9 PC10 PC11
## LC08_044034_20170614_B1 -0.1023702943 0.5365796233 0.127065695
## LC08_044034_20170614_B2 -0.1218742739 -0.7691469170 -0.196283512
## LC08_044034_20170614_B3 0.6640135096 0.0551533999 0.059318851
## LC08_044034_20170614_B4 -0.5347992170 0.2350928333 0.021665820
## LC08_044034_20170614_B5 -0.1995974299 -0.0311387747 0.004029261
## LC08_044034_20170614_B6 0.3828069102 0.0639560393 -0.021372642
## LC08_044034_20170614_B7 -0.2438645765 -0.0551104634 0.011338146
## LC08_044034_20170614_B8 0.0005337710 0.0005066492 -0.001773935
## LC08_044034_20170614_B9 -0.0009025984 -0.0006276713 0.001823281
## LC08_044034_20170614_B10 0.0039273450 -0.1709760476 0.686896213
## LC08_044034_20170614_B11 0.0433142125 0.1576520508 -0.684766019
screeplot(pca)
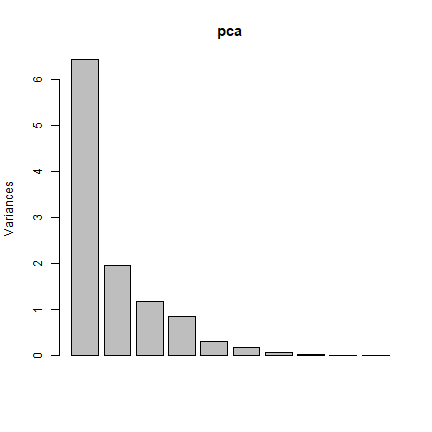
We use a function to restrict prediction to the first two principal components
pca_predict2 <- function(model, data, ...) {
predict(model, data, ...)[,1:2]
}
pci <- predict(landsat, pca, fun=pca_predict2)
plot(pci)
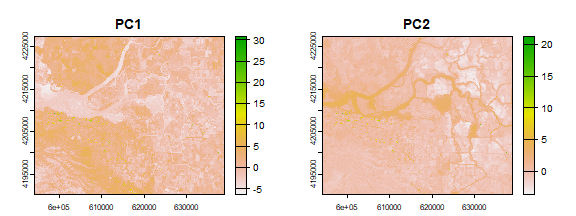
The first principal component highlights the boundaries between different land use classes. it is difficult to understand what the second principal component is highlighting. Lets try thresholding again:
# quick look at the histogram of second component
hist <- pci[[2]]
m <- c(-Inf,-3,NA, -3,-2,0, -2,-1,1, -1,0,2, 0,1,3, 1,2,4, 2,6,5, 6,Inf,NA)
rcl <- matrix(m, ncol = 3, byrow = TRUE)
rcl
## [,1] [,2] [,3]
## [1,] -Inf -3 NA
## [2,] -3 -2 0
## [3,] -2 -1 1
## [4,] -1 0 2
## [5,] 0 1 3
## [6,] 1 2 4
## [7,] 2 6 5
## [8,] 6 Inf NA
pcClass <- classify(pci[[2]], rcl)
Now plot the results
par(mfrow=c(1,2))
plotRGB(landsatFCC, stretch = "lin", main="False Color", mar=c(3.1, 3.1, 2.1, 2.1))
plot(pcClass, main="PCA")
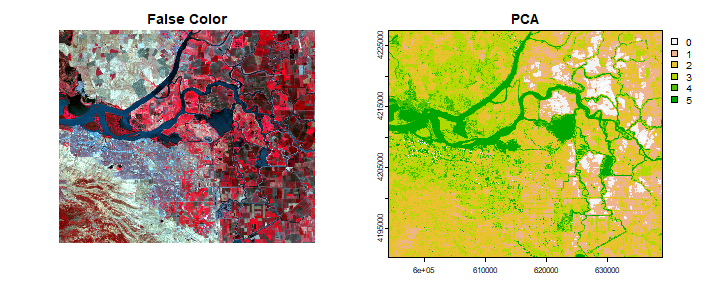
To learn more about the information contained in the vegetation and soil line plots read this paper by Gitelson et al. Details about PCA and an extension of PCA in remote sensing, Tasseled-cap Transformation.